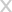If you’ve taken a geometry class, you're probably familiar with the concept of angles. Angles are formed when two lines intersect, and the amount of space between those lines is measured in degrees. You're probably also familiar with the different types of angles, such as right angles, acute angles, obtuse angles, and so on. In this article, we’ll be discussing a specific type of angle: alternate angles.

These angles are two angles that are equal to each other in measurement and are formed when two lines intersect. They’re situated on opposite sides of a transversal line but share the same vertex. Additionally, they are always congruent, which means that they have the same angle measurement.

Alternate Angle Theorem

The Alternate Angle Theorem states that if two parallel lines are cut by a transversal, then they form congruent alternate exterior and interior angles.

If you're still having trouble visualizing it, don't worry. We'll go over some examples below.

To see how alternate angle pairs are formed, consider the following example.

In this example, we have two parallel lines. These are lines a and b. The transversal line that bisects these two parallel lines is line l. Taken all together, these lines form eight angles in total, with four sets of alternate angles. Each angle in the figure has been labeled with a number.

In this figure, you’ll see that these angles are the ones opposite each other, sharing a single vertex where a parallel line and the transversal line intersect. The following angles are alternate angle pairs:

• Angles 1 and 4

• Angles 2 and 3

• Angles 5 and 8

• Angles 6 and 7

What are alternate interior angles?

Alternate interior angles are two angles that are located on the inside of the two parallel lines. See the figures below.

Above, you’ll see that angles 3 and 6 as well as angles 4 and 5 are alternate interior angle pairs.

What are alternate exterior angles?

Alternate exterior angles are two angles that are located on the outside of the two parallel lines as opposed to inside the lines. See the figures below.

Above, you’ll see that angles 1 and 8 as well as angles 2 and 7 are alternate exterior angle pairs.

Applications

There are many applications for alternate angles. Some of the most common are architecture, drafting, product design, and more.

You’ll also likely encounter angles like these when constructing buildings, renovating rooms in houses and other buildings, creating woodworking projects, and more. By understanding what an alternate angle is, you’ll be able to work with angles in your projects more easily.

With the help of tools like angle finders and protractors, you can take the measurements of alternate angle pairs and ensure that your work is progressing the way it should, or that you have accurate measurements. You can also make sure that all the different parts and pieces of your project fit together correctly.

Alternate vs adjacent angles

Angles can be adjacent or alternate if they share a common endpoint or vertex with another angle. It’s important to remember that alternate angles can share a common vertex and have the same measurement.

When two angles are adjacent, however, they share a common vertex as well as a common side. It’s also important to note that they do not always have the same measurement, but they do in certain situations. For example, two perpendicular lines can form four 90-degree angles, and all pairs of adjacent angles will measure the same.

If you work with the same figure with the parallel lines and transversal lines, see below for an example of adjacent angles.

As you can see, angles 1 and 2 as well as angles 6 and 8 are pairs of adjacent angles. Each pair shares a common side as well as a common vertex.

Additionally, the sum of the measurements of each pair of angles is 180 degrees. Angles 2 and 6 both measure 65 degrees, and angles 1 and 8 both measure 115 degrees. If you add the measurements of angles 1 and 2, the sum is 180 degrees.

However, it’s also important to note that not all pairs of adjacent angles have a total measurement of 180 degrees. Others will measure less or more.